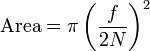Die Blendenzahl wird verwendet, um auszudrücken, wie viel Licht ein Objektiv aufnehmen kann, sodass 85 mm 1: 1,8 und 24 mm 1: 1,8 dieselbe Menge erfassen können. Hier ist f die Brennweite , und f / 1,8 bedeutet, dass der maximale Öffnungsdurchmesser im ersten Beispiel 47,2 mm und im zweiten 13,3 mm beträgt.

Was Sie hier berücksichtigen müssen, ist Da das 85-mm-Objektiv ein viel engeres Sichtfeld hat, muss es die gleiche Lichtmenge aus einem viel kleineren Bereich sammeln. Um die enge Sicht zu kompensieren, muss die Blende größer sein.

Wie viel die Die Blende muss größer sein und ist linear mit der Brennweite korreliert. Wir könnten sagen, dass ein 24-mm-Objektiv mit 13,3-mm-Blende so viel Licht sammeln kann wie ein 85-mm-Objektiv mit 47,2-mm-Blende, aber wenn man über die Blendenzahl spricht, ist dies viel einfacher zu bemerken.

Die Terminologie ist verwirrend, nicht wahr?

Die Blendenzahl eines 1: 1,8-Objektivs ist einfach 1,8 . Das ist gegeben durch N , nicht f . f ist die Brennweite.

f / 1,8 bedeutet wörtlich "Brennweite geteilt durch N ". Wenn Sie sich also auf f / 1.8 beziehen, ist dies nicht die Blendenzahl, sondern die Brennweite geteilt durch die Blendenzahl.

Um die Gleichungen weiter zu erläutern:

Die zweite Gleichung besagt dies Die Brennweite f geteilt durch den Öffnungsdurchmesser d ist die Blendenzahl N . Oder f / N = d . F / 1,8 bedeutet also wörtlich "Brennweite geteilt durch 1,8 (entspricht Durchmesser).

Wenn Sie sich die obere Gleichung ansehen, da f / N = d , dann f / 2N muss d / 2 sein (und d / 2 ist der halbe Durchmesser, ebenso wie der Radius der Öffnung). Und wir wissen, dass die Fläche eines Kreises ist pi r im Quadrat . pi mal f / 2N im Quadrat ist einfach der Bereich der Öffnungsöffnung.

Eine Gleichung gibt also den Durchmesser der Öffnungsöffnung an, und die andere verwendet die Grundgeometrie, um die Fläche der Öffnungsöffnung zu berechnen, die ein Kreis ist.

Ich denke, die Verwirrung rührt von zwei verschiedenen Dingen her, die die Erklärungen fälschlicherweise als "Lichtmenge" zusammenfassen.

Die wahre Lichtmenge, die ein Objektiv einlässt, ist nur eine Funktion des Blendenbereichs. Da die Fläche mit dem Quadrat des Durchmessers übereinstimmt, ist dies proportional zum Quadrat des Durchmessers.

Relevanter für die Belichtung ist jedoch nicht die Gesamtlichtmenge, die ein Objektiv sammeln kann, sondern die Helligkeit des fokussierten Bildes, das es erzeugt. Hier kommt die Brennweite ins Spiel. Angenommen, Sie haben ein 100-mm-Objektiv mit einer Blende von 25 mm Durchmesser (oder eine einstellbare Blende von 25 mm). Vergleichen Sie das jetzt mit einem 200-mm-Objektiv. Wenn das 200-mm-Objektiv auch eine Blende von 25 mm hat, lässt es die gleiche Lichtmenge ein. Dieselbe Lichtmenge, die vom Motiv kommt, wird jetzt doppelt so groß fokussiert, wodurch die vierfache Fläche eingenommen wird. Das bedeutet, dass das 200-mm-Objektiv mit 25-mm-Blende ein Bild erzeugt, das 1/4 so hell ist (2 Blendenstufen nach unten), verglichen mit dem 100-mm-Objektiv mit derselben 25-mm-Blende.

Beachten Sie, dass die Helligkeit von Das fokussierte Bild geht mit dem Quadrat der Brennweite nach unten, aber mit dem Quadrat des Aperturdurchmessers nach oben. Das heißt, wenn wir das Verhältnis der beiden nehmen würden, würden wir ein normalisiertes Maß dafür erhalten, wie hell das fokussierte Bild für Belichtungszwecke sein wird. Dieses Verhältnis ist genau das, was Blenden sind. Diese werden üblicherweise als f / n geschrieben, wie zum Beispiel f / 8.0 oder f / 11. Das ist nur ein Ausdruck. Die vollständige Gleichung lautet:

  Apertur = Brennweite / n  

Im ersten Beispiel eines 100-mm-Objektivs mit 25-mm-Apertur bedeutet dies:

  25 mm = 100 mm / 4  

Da das Schreiben und Sagen immer umständlich wird und es darum geht, sich nicht um die absolute Brennweite und Blende kümmern zu müssen sind, dies wird mit "f / 4" abgekürzt, wobei "f" sich auf die Brennweite der Linse bezieht und "4" das Verhältnis dieser Brennweite zum Aperturdurchmesser ist. Das zweite Beispiel war:

  25 mm = 200 mm / 8
 

oder "f / 8". Abgesehen von geringfügigen Lichtverlusten und anderen subtilen Effekten, die Sie die meiste Zeit ignorieren können, erzeugt ein Objektiv mit einer Blende von 1: 8 unabhängig von der Brennweite das gleiche helligkeitsfokussierte Bild wie ein anderes Objektiv bei 1: 8. Dies erklärt auch, warum lange Linsen tendenziell einen größeren Durchmesser haben. Ein 50-mm-Objektiv benötigt nur eine Blende von 12,5 mm, um 1: 4 zu erzielen. Ein 300-mm-Objektiv benötigt andererseits eine Apertur mit 75 mm Durchmesser, um das gleiche Helligkeitsbild des gleichen Motivs zu erzeugen. Das bedeutet, dass die Grundphysik besagt, dass ein 300-mm-Objektiv einen Durchmesser von mindestens 3 Zoll haben muss, um 1: 4 zu erzielen.

Wofür f in den Blendenwerten steht

f steht für die Brennweite des Objektivs. Eine 1: 1,8-Linse hat einen Eintrittspupillendurchmesser von D = 1: 1,8. Ein 85-mm-Objektiv mit einer Blende von 1: 1,8 hat einen Eintrittspupillendurchmesser von 85 / 1,8 = 47,2 mm. Eine 24-mm-Linse hat einen Pupillendurchmesser von 24 / 1,8 = 13,3 mm. Da die durch die Linse hindurchtretende Lichtmenge proportional zur Fläche der Eintrittspupille ist und diese proportional zum Quadrat ihres Durchmessers ist, sammelt die 85-mm-Linse anscheinend

(47,2 / 13,3) ^ 2 = (85/24) ^ 2 = 12,5

mal mehr Licht. Diese Überlegung gilt jedoch nur für die Lichtmenge, die von jedem einzelnen Punkt des Objekts gesammelt wird, nicht für die Gesamtlichtmenge, die aus dem Objektraum kommt.

Gleiches f -Nummer, gleiche Belichtung (unabhängig von f oder D)

Eine Sache, die ich auch verwirrend fand, ist, dass die Menge an Licht bei gesammelt wurde Der Sensor mit der gleichen Verschlusszeit von verschiedenen Objektiven mit der gleichen Blendenzahl ist der gleiche. Wie kommt es, wenn ein Objektiv deutlich größer als das andere ist?

Hier ist eine Illustration dessen, was in der Kamera passiert:

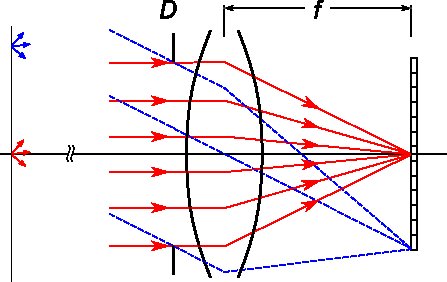
Der Einfachheit halber Es wird angenommen, dass sich das Objekt im Unendlichen befindet, so dass alle Strahlen vom selben Objektpunkt parallel zueinander kommen. Die roten durchgezogenen Strahlen treten parallel zu ihrer Achse in die Linse ein und sind alle in der Mitte des Rahmens fokussiert. Die blau gestrichelten Strahlen sind parallel zueinander, aber nicht parallel zur Achse. Sie alle konzentrieren sich auf den Rand des Rahmens. Somit bestimmt die Rahmengröße zusammen mit der Brennweite des Objektivs das Sichtfeld des Objektivs.

(Beachten Sie, dass das Sichtfeld im Objektraum ein ist, da ich die Objektentfernung unendlich gemacht habe eckig.)

Wenn wir das Objektiv auf ein Objektiv mit längerer Brennweite bei gleichbleibender Bildgröße ändern, verringert sich das Sichtfeld des Objektivs:

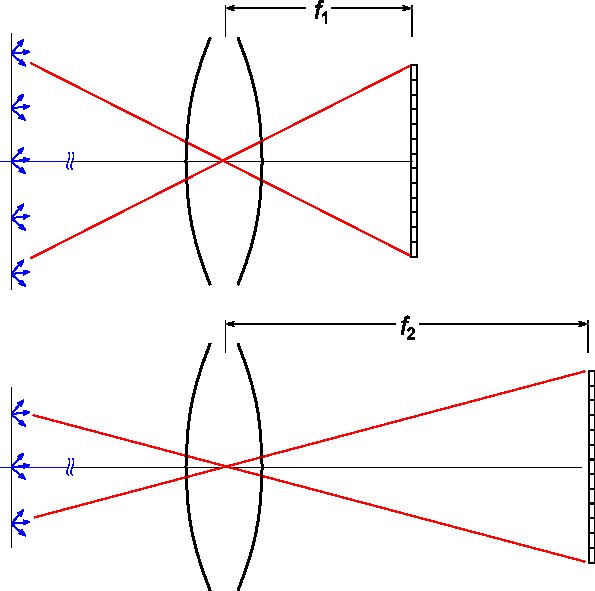
Während die Linse immer noch die gleiche Lichtmenge von jedem Punkt im Objektraum sammelt, ist die Größe dieses Raums kleiner, so dass die Gesamtlichtmenge, die den Film oder Detektor erreicht, verringert wird . Diese Verringerung ist proportional zur Erhöhung der Brennweite, d. h. die Lichtmenge mit demselben D wird um einen Faktor von (f2 / f1) ^ 2 verringert. (Es ist quadratisch, weil wir die Verkleinerung des Sichtfelds in beide Richtungen berücksichtigen müssen.)

Wenn wir jetzt D um f2 / f1 erhöhen, werden wir es erneut tun Sammle die alte Lichtmenge (da sie proportional zu D ^ 2 ist). Die Blendenzahl wird: D2 / f2 = [D1 * (f2 / f1)] / f2 = D1 / f1. Wenn wir also die gleiche Lichtmenge sammeln möchten, während wir die Brennweite ändern, müssen wir die Blendenzahl konstant halten.

Die Rahmengröße ist wichtig

Der letzte interessierende Parameter ist die Rahmengröße. Nehmen Sie eine Kompaktkamera mit demselben Blendenobjektiv wie eine Vollformat-Spiegelreflexkamera. Wenn die Größe des Objektivs und des Sensors proportional zur Brennweite verkleinert wird, haben die beiden Kameras das gleiche Sichtfeld. Die Kompaktkamera sammelt weniger Licht als die Spiegelreflexkamera, da das Objektiv kleiner ist. Der Sensor erhält jedoch immer noch den gleichen Belichtungswert, da Belichtung die Lichtmenge pro Flächeneinheit ist.

Wenn die beiden Kameras dieselbe Auflösung haben, ist die Belichtung gleich, aber die tatsächliche Lichtmenge auf jedem Pixel ist mit der größeren Spiegelreflexkamera größer, was zu einem geringeren Rauschen führt.

Jedes Objektiv mit 1: 2,8 sollte die gleiche Lichtmenge an die Kamera liefern. Bestimmte Objektive müssen jedoch härter arbeiten, um dorthin zu gelangen.

Es ist technisch nicht korrekt, aber ich fand, dass der beste Weg, um die Blendenzahl zu verstehen, darin besteht, sie als Repräsentation der Lichtmenge zu betrachten hat verloren. Bei 1: 2,8 verlieren Sie also nur das 2,8-fache der Lichtmenge, während Sie bei 1: 11 das 11-fache der Lichtmenge verlieren. *

Ein Teleobjektiv hat naturgemäß weniger Licht als ein Weitwinkelobjektiv. Je schwieriger das Objektiv arbeiten muss, um Lichtverlust zu vermeiden, desto mehr Glas benötigen Sie, um so viel Licht wie möglich einzufangen. Sie können also ein 55-250 f / 4-5,6 mit einem Gewicht von etwa 1 Pfund und einem Gewicht von 6-8 Zoll verwenden. während ein 70-200 mm 1: 2,8 6 Pfund wiegt und über 12 Zoll lang ist.

* Dies ist aus mathematischer Sicht nicht die richtige Vorgehensweise, kann Ihnen jedoch beim praktischen Verständnis helfen.